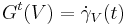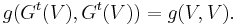Closed geodesic

In differential geometry and dynamical systems, a closed geodesic on a Riemannian manifold M is the projection of a closed orbit of the geodesic flow on M.

1 Examples
2 Definition
3 See also
4 References

Examples

On the unit sphere, every great circle is an example of a closed geodesic. On a compact hyperbolic surface, closed geodesics are in one-to-one correspondence with non-trivial conjugacy classes of elements in the Fuchsian group of the surface. A prime geodesic is an example of a closed geodesic.

Definition

Geodesic flow is an 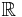$\mathbb R$ -action on tangent bundle T(M) of a manifold M defined in the following way

$G^t(V)=\dot\gamma_V(t)$

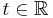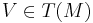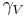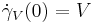where $t\in \mathbb R$ , $V\in T(M)$ and $\gamma_V$ denotes the geodesic with initial data $\dot\gamma_V(0)=V$ .

It defines a Hamiltonian flow on (co)tangent bundle with the (pseudo-)Riemannian metric as the Hamiltonian. In particular it preserves the (pseudo-)Riemannian metric $g$ , i.e.

$g(G^t(V),G^t(V))=g(V,V).\,$

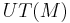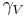That makes possible to define geodesic flow on unit tangent bundle $UT(M)$ of the Riemannian manifold $M$ when the geodesic $\gamma_V$ is of unit speed.

References

Besse, A.: "Manifolds all of whose geodesics are closed", Ergebisse Grenzgeb. Math., no. 93, Springer, Berlin, 1978.

Closed geodesic

Contents

Examples

Definition

See also

References